Question

I’m in AP Calculus AB. Can you help me solve this showing steps?I’m not exactly sure how to do this.

Answer 1

We need to find the derivative of a function, but if we look at the function is a quotient. Then we can use the rule for the derivative of a quotient:

`\begin{gathered} f(x)=(g(x))/(h(x)) \\ \text{Then,} \\ (df)/(dx)=(g^(\prime)h-h^(\prime)g)/(h^2) \end{gathered}`

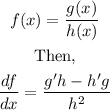
In this case, we have:

`f(x)=(\csc (x))/(x^2)`

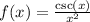
We can call:

`\begin{gathered} g(x)=\csc (x) \\ h(x)=x^2 \end{gathered}`

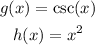
Now we apply the rule:

`(df)/(dx)=((dg)/(dx)h-(dh)/(dx)g)/(h^2)`

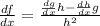
We know that the derivative of h(x) = x^2 is 2x, and the derivative of g(x) = csc(x) is [-cot(x)csc(x)]

Replacing the values:

`(df)/(dx)=(-\cot (x)\csc (x)\cdot x^2-2x\cdot\csc (x))/((x^2)^2)`

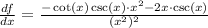
Simplifying:

We can factor out csc(x)*x in the numerator and solve the square in the denominator

`(df)/(dx)=(x\csc (x)(-x\cot (x)-2))/(x^4)`

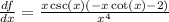
Finally, we can factor the (-1) inside the parentheses and cancel out the x in the numerator:

`(df)/(dx)=-(\csc (x)(x\cot (x)+2))/(x^3)`

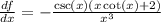
And this is the final answer.