Answer:

Explanation:
Given :
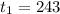
Expression :

Put n = 1
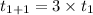
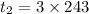
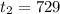
Put n = 2

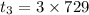
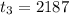
Put n = 3
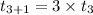
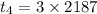
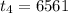
Continuing in this manner we will get the geometric sequence :
243,729,2187,6561 ........
Formula for nth term of G.P. :
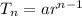
a= 243
r = common ratio between the consecutive terms .
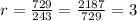
Substituting values in the formula :

Hence the general term of the sequence is
