I am setting the length equal to L and the width equal to L - 3. We can do this because we know the width is equal to 3 cm less than the length. Because the area of a rectangle is equal to length times width, we can set up this equation:
L * (L - 3) = 70
Now, we can solve for L. We start by distributing the L.
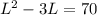
Next, we subtract 70 from both sides.
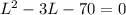
Now, we can factor this equation. It becomes:
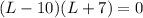
The zeros of this equation are:
L = 10, -7
Since the rectangle can't have a width of -7, we use positive 7 instead. So, the dimensions of this rectangle are 10 cm X 7 cm