Question

If y = 2x - 8 what is the minimum value of the product xy

Answer 1

The minimum value of the product xy is at (2, -8)

Vertex of a parabola

Given the functin y = 2x - 8

The expression xy is given as:

xy = x (2x-8)

xy = 2x² - 8x

The x-coordinate of the vertex os given as:
x = -b/2a

x = -(-8)/2(2)

x = 8/4

x = 2

Substitute x = 2 into the function to get "y'

y = 2x² - 8x

y = 2(2)² - 8(2)

y = 8 - 16

y = -8

Hence the minimum value of the product xy is at (2, -8)

Learn more on vertex of parabola here:

Answer 2

the minimum value of product is -8

Explanation:

We have been given the function y = 2x-8 and we have to find the minimum value of the xy.

Plugging the value of y in the product

`f(x)=x(2x-8)\\\\f(x)=2x^2-8x`

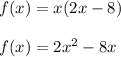
f(x) represents a upward parabola and we know that for a upward parabola, the minimum point is the vertex.

So in order to find the minimum value we find the y coordinate of the vertex of the parabola.

x-coordinate of the parabola is given by

`-(b)/(2a)\\\\=-(-8)/(2\cdot2)\\\\=2`

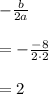
y -coordinate of the parabola is

`y=f(2)=2(2)^2-8(2)\\\\=8-16=-8`

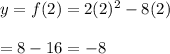
Hence, the vertex is (2,-8)

Therefore, the minimum value of product is -8