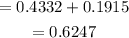Let X be the number of heartbeats of any individual in the group.
The variable X is normally distributed with mean 74 beats per minute,

The standard deviation is 2 beats per minute,
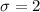
Consider the formula of z-score corresponding to any value of X=x as,
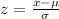
It is required to find the probability that the number of heartbeats of a randomly selected person lies between 71 and 75.
This can be obtained as follows,
![\begin{gathered} P(71From the Standard Normal Distribution Table,[tex]\begin{gathered} \phi(0.5)=0.1915 \\ \phi(1.5)=0.4332 \end{gathered}]()
Substitute the values and simplify,