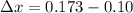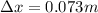Answer:
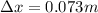
Step-by-step explanation:
Potential energy of the spring is given by the formula
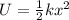
so here we can say that the potential energy stored in the spring is directly depends upon the square of the deformation of the spring
So here we can say that
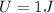
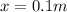
so we have
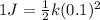
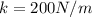
now if we have to increase the potential energy to triple of this initial value
then we have
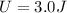
so we will have
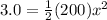
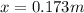
so we have to further compress the spring by