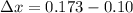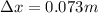Question

Suppose a 0.3-kg mass on a spring that has been compressed 0.10 m has elastic potential energy of 1.0 j. how much further must the spring be compressed to triple the elastic potential energy?

Answer 1

not sure what that mass was supposed to do there

if the spring was compressed 0.1m and has E=1.0 J
than
E=F*d/2=k*d*d/2 wich means

k=2*E/d^2= 2* 1J/ 0.01m^2= 200 N/m
so
for E=3J we have E=k*d^2/2 =>
d= sqrt(2*E/k)=sqrt(2*3J/200 N/m)= sqrt (0.03) m = 0.17 m

this means that the spring has to be compressed an aditional 0.07 m to triple the energy
(still not sure what that 0.3 kg mass has to do with it)

Answer 2

`\Delta x = 0.073 m`

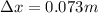
Step-by-step explanation:

Potential energy of the spring is given by the formula

`U = (1)/(2)kx^2`

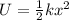
so here we can say that the potential energy stored in the spring is directly depends upon the square of the deformation of the spring

So here we can say that

`U = 1 J`

`x = 0.1 m`

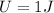
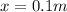
so we have

`1 J = (1)/(2)k(0.1)^2`

`k = 200 N/m`

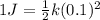
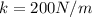
now if we have to increase the potential energy to triple of this initial value

then we have

`U = 3.0 J`

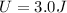
so we will have

`3.0 = (1)/(2)(200) x^2`

`x = 0.173 m`

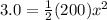
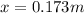
so we have to further compress the spring by

`\Delta x = 0.173 - 0.10`

`\Delta x = 0.073 m`