Question

PLEASE HELP!!!!
Which of these pair of functions are inverse functions?

Answer 1

Option B and C are correct.

Explanation:

Inverse function: If both the domain and the range are R for a function f(x), and if f(x) has an inverse g(x) then:

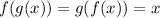`f(g(x)) = g(f(x)) = x` for every x∈R.

Let
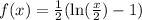`f(x) = (1)/(2)(\ln((x)/(2)) -1)` and
`g(x) = 2e^(2x+1)`

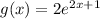
Use logarithmic rules:

• 
  `ln e^a = a`

• 
  `e^(lnx) = x`

• 
  `\ln a^b = b\ln a`

then, by definition;

`f(g(x)) = f(2e^(2x+1)) =(1)/(2)(\ln((2e^(2x+1))/(2))-1)` =
`(1)/(2)(\ln(e^(2x+1)}){-1) = (1)/(2) (2x+1-1) =(1)/(2)(2x) = x`

`g(f(x)) = g((1)/(2)(\ln((x)/(2)) -1)) = 2e^{2({(1)/(2)(\ln((x)/(2)) -1})+1`
`2e^{(\ln((x)/(2)) -1+1}=2e^{\ln((x)/(2))} =2\cdot (x)/(2) = x`

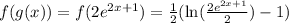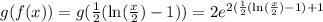
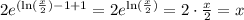
Similarly;

for
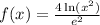`f(x) = (4 \ln(x^2))/(e^2)` and
`g(x) = e^{(e^2 \cdot x)/(8) }`

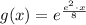
then, by definition;

`f(g(x)) = f(e^{(e^2 \cdot x)/(8)}) =\frac{4 \ln {((e^2 \cdot x)/(8))^2}}{e^2}` =
`\frac{8 \ln {((e^2 \cdot x)/(8))}}{e^2} =(8(e^2\cdot x)/(8) )/(e^2)=(8e^2 \cdot x)/(8e^2)=x`

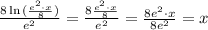
Similarly,

g(f(x)) = x

Therefore, the only option B and C are correct. As the pairs of functions are inverse function.