Question

What are two possible solutions using square root? A) 3(x-5)^2=48B) 2x^2-56=42

Answer 1

A)

The equation given, is

`3(x-5)^2=48`

To solve for x, we first divide both sides by '3',

`\begin{gathered} (3(x-5)^2)/(3)=(48)/(3) \\ (x-5)^2=16 \end{gathered}`

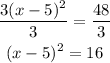
Now, we take the square root and solve for the value(s) of x:

`\begin{gathered} \sqrt[]{(x-5)^2}=\pm\sqrt[]{16} \\ x-5=\pm4 \\ x=\pm4+5 \\ x=1,9 \end{gathered}`

Thus, the solutions are

`\begin{gathered} x=1 \\ x=9 \end{gathered}`

B)

The equation to solve:

`2x^2-56=42`

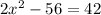
Let's solve for x. The algebra is shown below:

`\begin{gathered} 2x^2-56=42 \\ 2x^2=42+56 \\ 2x^2=98 \\ x^2=49 \\ \sqrt[]{x^2}=\pm\sqrt[]{49} \\ x=7,-7 \end{gathered}`

Thus, the solutions are

`\begin{gathered} x=-7 \\ x=7 \end{gathered}`