Question

Use the information provided to write the vertex form equation of each parabola.x² - 12x + y + 40 = 0

Answer 1

Vertex form of Parabolas

Initial explanation

We want to write the following parabola in the vertex form equation:

x² - 12x + y + 40 = 0

↓ taking x², - 12x and 40 to the right side

y = -x² + 12x - 40

This means that we want to transform our equation into another equation like this:

`y=a(x-h)^2+k`

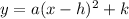
where a, h and k are numbers.

In order to do so we rewrite the equation completing the square.

Step 1: finding a

We rewrite our equation so the first term is positive:

y = -x² + 12x - 40

↓

y = -(x² - 12x + 40)

Step 2: finding h

We want to rewrite x² - 12x + 40 completing the square.

We know that:

`(x-h)^2=x^2-2xh+h^2`

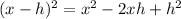
Since 2 · 6 = 12, then in this case, we have that:

x² - 12x + 40 = x² - 2 · 6x + 40

Then, in this case h = 6

Since

h² = 6² = 36

we add and subtract 36 in our question:

x² - 2 · 6x + 40 = x² - 2 · 6x + (36 - 36) + 40

we are going to use the terms that form the square:

x² - 2 · 6x + 36 - 36 + 40

= [x² - 2 · 6x + 36] - 36 + 40

↓ since -36 + 40 = 4

= [x² - 2 · 6x + 36] + 4

Since

(x - 6)² = [x² - 2 · 6x + 36]

then

[x² - 2 · 6x + 36] + 4

= (x - 6)² + 4

Step 3: finding the final equation

Then, we have that

y = -(x² - 12x + 40)

where, we found that in square form:

x² - 12x + 40 = (x - 6)² + 4

Then, replacing it, we have

y = -(x² - 12x + 40)

↓replacing (x - 6)² = [x² - 2 · 6x + 36]

y = -((x - 6)² + 4)

↓multiplying -1

y = -(x - 6)² - 4

Then, we have found an equation of the vertex form for this parabola.

Answer: y = -(x - 6)² - 4