Question

4) Landon is standing in a hole that is 6.5 m deep. he throws a rock, and it goes up into the air, out of the hole, and then lands on the ground above. The path of the rock can be modeled by the equation y=-0.05x^2+4.5x-6.5, where x is the horizontal distance of the rock, in meters, from landon and y is the height, in meters, of the rock above the ground. How far horizontally from landon will the rock land? Round your answer to the nearest hundredth of a meter. (1 point)

a. 82.03 m <----
b. 6.50 m
c. 90.00 m
d. 88.53 m

Answer 1

the answer is b.6.50m

Answer 2

The rock will land 88.53 horizontally far from Landon.

Explanation:

The path of the rock can be modeled by the equation:
`y=-0.05x^2+4.5x-6.5`

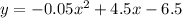
Where x is the horizontal distance of the rock, in meters, from landon and y is the height, in meters, of the rock above the ground.

Now we are supposed to find How far horizontally from landon will the rock land

when the rock land so y becomes 0

So, substitute y =0 is the given equation.

`0=-0.05x^2+4.5x-6.5`

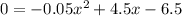
Use quadratic formula :
`x=(-b\pm√(b^2-4ac))/(2a)`

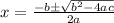
Substitute a = -0.05

b = 4.5

c= -6.5

So,
`x=(-4.5\pm√((4.5)^2-4(-0.05)(-6.5)))/(2(-0.05))`

`x=(-4.5\pm4.35315977194)/(-0.1)`

`x=(-4.5+4.35315977194)/(-0.1),(-4.5-4.35315977194)/(-0.1)`

`x=1.47,88.531`

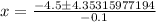
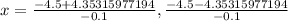
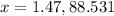
Thus It will be 88.53m horizontal distance from Landon when it strikes the ground.

The rock will be 1.47m horizontal distance from Landon where it exits the hole.

Hence Option D is correct.

The rock will land 88.53 horizontally far from Landon.