Answer:
x = 25
Explanation:
Given :
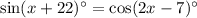
We have to find the value of x.
Consider the given
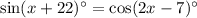
We know,
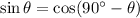
Consider the left side
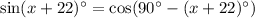
thus,
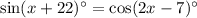 becomes,
becomes,

Simplify for x,
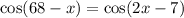
Thus, 68 - x = 2x - 7
Adding x both side , we have
68 = 3x - 7
Adding 7 both side, we have,
75 = 3x
Divide both side by 3, we have,
x = 25
Thus, x = 25