Answer:
Option B The graph of
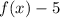 is a vertical shift of
is a vertical shift of
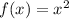 five units down.
five units down.
Explanation:
we have
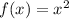
Is a vertical parabola open upward with the vertex at
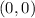
Let

so

Is a vertical parabola open upward with the vertex at
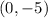
The rule of the translation of f(x)-----> g(x) is equal to

That means-----> The translation is
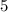 units down
units down
therefore
The graph of
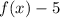 is a vertical shift of
is a vertical shift of
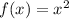 five units down.
five units down.