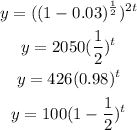Question

Can you tell me if this is right. I am confused, please see attachment.

Answer 1

All the function as exponential and they can be written in the form:

`y=A\cdot b^t`

When written in thif form, we can check if the function describe an exponential growth or decay by checking "b".

`\begin{gathered} if\, 01\to exponential\, growth \end{gathered}`

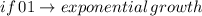
Let's start with the two that are already in this form:

`y=0.1(1.25)^t`

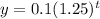
Here, b = 1.25. Since b > 1, this describe an exponential growth.

`y=426(0.98)^t`

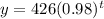
b = 0.98. Since 0 < b < 1, this describe an exponential decay.

Now, this one is almost in this form:

`y=2050((1)/(2))^t`

We just need to turn b = 1/2 to decimal to be sure. 1/2 is 0.5, so b = 0.5. Since 0 < b < 1, this describe an exponential decay.

This one, we need to evaluate the expression inside parenthesis:

`y=100(1-(1)/(2))^t`

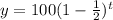
Here, b is:

`b=1-(1)/(2)=1-0.5=0.5`

Since 0 < b < 1, this describe an exponential decay.

Lastly,, we have the following:

`y=((1-0.03)^{(1)/(2)})^(2t)`

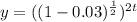
First, le'ts make the substraction:

`y=((0.97)^{(1)/(2)})^(2t)`

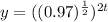
Now, notice that when we have a multiplication in an exponent, we can do the following:

`a^(c\cdot d)=(a^c)^d`

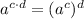
Thus, we can do the contrary. So,

`y=((0.97)^{(1)/(2)})^(2t)=(0.97)^{(1)/(2)\cdot2t}=(0.97)^t`

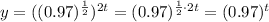
Notice that we don't have anything in the place of "A", but this means that A = 1. This doesn't change b, that is, in this case equal to 0.97. Since 0 < b < 1, this describe an exponential decay.

So, the function that describe exponential growth is:

`0.1(1.25)^t`

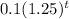
And the functions that describe exponential decay are:

`\begin{gathered} y=((1-0.03)^{(1)/(2)})^(2t) \\ y=2050((1)/(2))^t \\ y=426(0.98)^t \\ y=100(1-(1)/(2))^t \end{gathered}`