Answer: 25,000
Step-by-step explanation:
Let's call X the part of the payment invested at 10% annual and Y the part of the payment invested at 8% annual interest.
Since the total payment is 40,000, we can write the following equation:
X + Y = 40,000
On the other hand, the annual interest can be calculated as:
I = P*r
Where P is the initial value and r is the annual interest rate
Then, the total annual interest can be calculated as:
I = X*0.1 + Y*0.08
Since the total annual interest is $3500, we can write the following equation:
3500 = 0.1X + 0.08Y
Now, we can solve for X in the first equation and replace it on the second as:
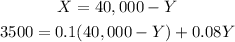
Solving for Y, we get:
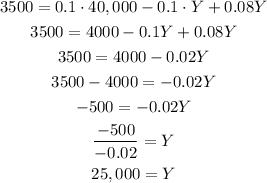
Therefore, 25,000 was invested at the 8% rate