Question

EXPLAIN THE SECOND PART.......

Answer 1

`\tan^2\theta-\sin^2\theta=(\sin^2\theta)/(\cos^2\theta)-\sin^2\theta`

`=\sin^2\theta\left(\frac1{\cos^2\theta}-1\right)`

`=\sin^2\theta(\sec^2\theta-1)`

`=\sin^2\theta\tan^2\theta`

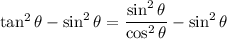
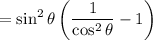
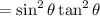
Now if
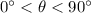
`0^\circ<\theta<90^\circ`, then both
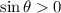
`\sin\theta>0` and
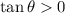
`\tan\theta>0`. Adding two positive numbers gives another positive number, so
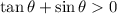
`\tan\theta+\sin\theta>0`. Why this is useful will be apparent shortly.

Back to the identity:


`\tan^2\theta-\sin^2\theta=\tan^2\theta\sin^2\theta`

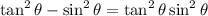
Factorizing the left hand side, we have


`(\tan\theta-\sin\theta)(\tan\theta+\sin\theta)=\tan^2\theta\sin^2\theta`

Now, any number squared will be positive, which means the right hand side is necessarily greater than 0.

We showed earlier that
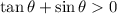
`\tan\theta+\sin\theta>0`. So we understand that we have


`\underbrace{(\tan\theta-\sin\theta)}_?\underbrace{(\tan\theta+\sin\theta)}_+=\underbrace{\tan^2\theta\sin^2\theta}_+`

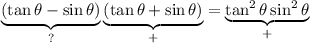
The only way to multiply a number by a positive number to get yet another positive number is to have the first number also be positive, which means


`\tan\theta-\sin\theta>0`

and from this it follows that


`\tan\theta>\sin\theta`

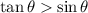
in the provided region.