Question

Find y if the slope between (-3,y) and (5,9) is 1

Answer 1

To find the value of y for point (-3,y), knowing that the line that links the said point and point (5,9) has a slope equal to 1, first, you have to determine the equation of the line.

For this, you have to use the point-slope form:

`y-y_1=m(x-x_1)`

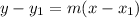
Where

m is the slope of the line

(x₁,y₁) are the coordinate of one point of the line

Replace the formula with x₁=5, y₁=9, and m=1

`y-9=1(x-5)`

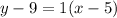
Now let's write the equation in slope-intercept form:

-Distribute the multiplication on the parentheses term:

`\begin{gathered} y-9=1\cdot x-1\cdot5 \\ y-9=x-5 \end{gathered}`

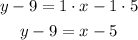
-Pass "-9" to the right side of the equal sign by applying the opposite operation "+9" to both sides of it:

`\begin{gathered} y-9+9=x-5+9 \\ y=x+4 \end{gathered}`

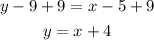
Once the equation of the line is determined, replace it with x=-3 to calculate the corresponding y-value:

`\begin{gathered} y=x+4 \\ y=-3+4 \\ y=1 \end{gathered}`

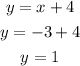
The value of y is 1, you can write the coordinate pair as (-3,1)