Answer: $396,800
Explanation:
Given: The initial investment = $6200
The constant ratio = 2
Time takes to double the amount (Time period )= 13
The number of time periods in 78 years =
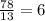
The exponential growth equation is given by :-
 , whre A is the initial amount , b is the constant ratio and x is the number of time periods .
, whre A is the initial amount , b is the constant ratio and x is the number of time periods .
Now, the investment worth after 78 years will be given by :-

Hence, The investment worth after 78 years is $396,800.