Question

Eric is participating in a pumpkin-launching competition using a homemade air cannon. He collected three points of data from his launch, but wants to determine some specifics about the launch from the data. The table contains the data he collected.Time from Launch, t (seconds)Height of Pumpkin, h (feet)00227210.50Use this data to complete the task.Part AThe motion of a projectile, comparing height over time, can be modeled using a quadratic function. To model this situation with a quadratic function, first identify two of the factors of the quadratic by identifying the zeros in the data points.Part BNow that you have two factors, you need to determine what constant to multiply them by to find the actual function. To do this, let c represent the unknown constant, t represent time, and h represent height. Then, use the middle data point to find the value of c and write a function to model the situation. Show your work.Part CAll projectile motion situations can be modeled by the function h(t)=1/2at^2+v0t+h0, where a represents the vertical acceleration acting on the projectile (this is generally the acceleration due to gravity), represents the initial vertical velocity of the projectile, and represents the initial height of the object.Using this information, what is the initial vertical velocity of the pumpkin when it is launched?Part DThe maximum height of the pumpkin will occur exactly halfway between the zeros of the function. Determine the maximum height Eric’s pumpkin will reach during its flight. Show your work.

Answer 1

PART A:

The zeros of the function are the values of t where we have h = 0.

Looking at the table, the zeros are t = 0 and t = 10.5

PART B:

Let's write the function using the factored form of the quadratic equation:

`h(t)=c(t-t_1)(t-t_2)_{}`

Since the zeros are 0 and 10.5, we have t1 = 0 and t2 = 10.5, so:

`h(t)=c\cdot t\cdot(t-10.5)`

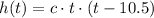
Now, using the point (2, 272) from the table, we have:

`\begin{gathered} 272=c\cdot2\cdot(2-10.5) \\ 272=2c\cdot(-8.5) \\ -17c=272 \\ c=-16 \end{gathered}`

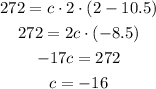
So our function is:

`h(t)=-16\cdot t\cdot(t-10.5)`

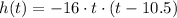
PART C:

First let's expand our function to the standard form:

`\begin{gathered} h(t)=-16t(t-10.5) \\ h(t)=-16t^2+168t+0 \end{gathered}`

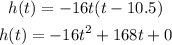
Comparing with the given model, we have V0 = 168 ft/s (because the coefficient multiplying the variable t is 168 in our function and V0 in the given model).

PART D:

First, let's calculate the average value between the zeros:

`t_v=(0+10.5)/(2)=5.25`

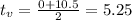
Using this value of t in the function, we have:

`\begin{gathered} h(t_v)=-16\cdot5.25\cdot(5.25-10.5) \\ h(t_v)=441\text{ ft} \end{gathered}`

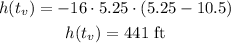
So the maximum height is 441 ft.