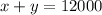Question

Leroy invested 12,000 into two different bank accounts. One account (x) gives Leroy 1.5% interest yearly and the other account (y) give Leroy 3% interest yearly. At the end of one year Leroy had earned $300 in interest. Which system of equations could be used to solve for how much money Leroy invested in the two accounts?

Answer 1

0.015x+0.03(12000-x)=300
Solve for x
X=4000 at 1.5%

12000-4000=8000 at 3%

Answer 2

Answer: The system of equations is,

`0.15x+0.03y=300`

`x+y=12000`

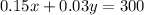
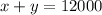
Explanation:

For first account,

Investment = x,

Annual rate of interest = 1.5 %

Time = 1 year

Thus, the total interest by one account,

`I_1=(x* 1.5* 1)/(100)=0.015x`

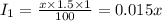
Now, for second account,

Investment = y

Annual rate of interest = 1.5%

Time = 1,

Hence, the interest by the second account,

`I_2=(y* 3* 1)/(100)=0.03y`

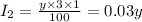
Thus, the total interest,

`I=I_1+I_2=0.015 x + 0.03y`

According to the question,

`I=300`

`\implies 0.15x+0.03y = 300`

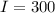
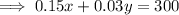
Now, total investment = 12000,

⇒ x + y = 12000

Hence, the required system of equations, to solve for how much money Leroy invested in the two accounts is,

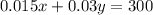`0.015x+0.03y= 300`,

`x+y=12000`