Question

Write the equation for f(x) and g(x). Then identify the reflection that transforms the graph of f(x) to the graph of g(x).

Answer 1

Given the figure of the functions f(x) and g(x)

The graph of the function is the shown lines

The equation of f(x):

As shown the line of f(x) passes through the points: (-2, 0) and (0, -1)

The slope of the line will be:

`slope=(rise)/(run)=(y_2-y_1)/(x_2-x_1)=(-1-0)/(0-(-2))=(-1)/(2)`

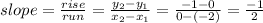
The y-intercept = -1

so, the equation of f(x) =

`f(x)=-(1)/(2)x-1`

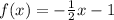
The equation of g(x):

As shown the line of g(x) passes through the points: (-2, 0) and (0, 1)

The slope of the line will be:

`slope=(rise)/(run)=(y_2-y_1)/(x_2-x_1)=(1-0)/(0-(-2))=(1)/(2)`

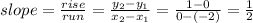
The y-intercept = 1

So, the equation of g(x) will be:

`g(x)=(1)/(2)x+1`

Identify the reflection that transforms the graph of f(x) to the graph of g(x).

As shown, the functions are symmetric around the x-axis

And as we can see for the same value of x: g(x) = -f(x)

So, the type of transformation is: Reflection over the x-axis