In order to determine which equation represents the boundary, replace the values of the coordinates of the given points, into the choices for the equations, and then verify if the left hand side matches with the right hand side.
For points (35,0) and (5,0) you have:
x = 35
y = 0
x = 5
y = 0
Then, for the first answer choice we have:
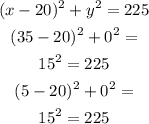
As you can notice, the equation matches for values of x and y.
Then, there is no necessary to verify for the other choices.
Hence, the equation (x - 20)^2 + y^2 = 225 represents the boundary that the sprinkler covers.