Answer: The measure of ∠BEC = 50°.
Explanation:
Since we have given that
∠BEC is formed inside a circle by two intersecting chords.
and the value of minor arc BD = 94
The value of major arc CA = 166
We need to find the measure of ∠ BEC.
As we know theorem, the angle AEC is equal to half the sum of the intercepted arcs.
We will use to find the intercepted angles when two chords got intersected i.e.

Since ∠ AEC and ∠BEC are supplementary angles.
So, it becomes,
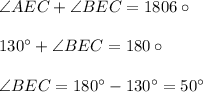
Hence, the measure of ∠BEC = 50°.