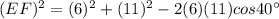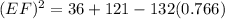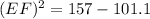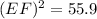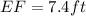Question

LAW OF COSINES HELP. 2 Questions. Serious help ONLY. (will report if needed)

1. What is the length of AB, to the nearest tenth of a meter?

4.4 m

6.5 m

8.6 m

8.9 m

2. What is the length of EF?
Enter your answer as a decimal in the box. Round only your final answer to the nearest tenth.

ft

Answer 1

`\bf \textit{Law of Cosines}\\ \quad \\ c^2 = {{ a}}^2+{{ b}}^2-(2{{ a}}{{ b}})cos(C)\implies c = \sqrt{{{ a}}^2+{{ b}}^2-(2{{ a}}{{ b}})cos(C)}\\\\ -----------------------------\\\\ AB = \sqrt{{{ 7}}^2+{{ 6}}^2-2(7\cdot 6)cos(83^o)}\\\\ -----------------------------\\\\ EF = \sqrt{{{ 11}}^2+{{ 6}}^2-2(11\cdot 6)cos(40^o)}`

the angles are in degrees, thus, make sure your calculator is in Degree mode

Answer 2

Explanation:

(A) From the given figure, it is given that ABC is a triangle and AC=6m, BC=7m and ∠C=83°.

thus, using the law of cosines in the given triangle ABC, we get

`(AB)^2=(AC)^2+(BC)^2-2(AB)(BC)cosC`

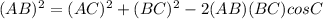
Substituting the given values, we have

`(AB)^2=(6)^2+(7)^2-2(6)(7)cos83^(\circ)`

`(AB)^2=36+49-84(0.121)`

`(AB)^2=85-10.164`

`(AB)^2=74.836`

`AB=8.6m`

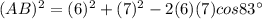
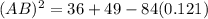
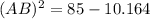
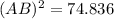
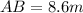
Thus, option (C) is correct.

(B) From the given figure, it is given that ABC is a triangle and DE=6ft, DF=11ft and ∠D=40°.

thus, using the law of cosines in the given triangle ABC, we get

`(EF)^2=(DE)^2+(DF)^2-2(DE)(DF)cosD`

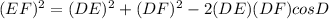
Substituting the given values, we have

`(EF)^2=(6)^2+(11)^2-2(6)(11)cos40^(\circ)`

`(EF)^2=36+121-132(0.766)`

`(EF)^2=157-101.1`

`(EF)^2=55.9`

`EF=7.4ft`