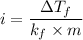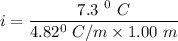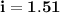Answer:
Step-by-step explanation:
From the given information:
TO start with the molarity of the solution:
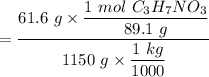
= 0.601 mol/kg
= 0.601 m
At the freezing point, the depression of the solution is
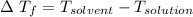
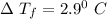
Using the depression in freezing point, the molar depression constant of the solvent
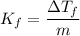
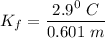
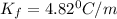
The freezing point of the solution
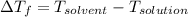
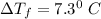
The molality of the solution is:
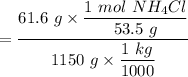
Molar depression constant of solvent X,
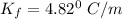
Hence, using the elevation in boiling point;
the Vant'Hoff factor