Which system of linear inequalities is represented by the graph?

Question

asked Aug 1, 2018 129k views

2 Answers

Dukable · Answer 1 · 2018-08-05T20:22:50+0000

Answer:

The correct option is 2.

Explanation:

From the given graph it is clear that the y-intercept of red line is 1 and y-intercept of blue line is 4.

The red line passes through the points (0,1) and (5,0). So, the slope of red line is

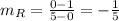
m_R=(0-1)/(5-0)=-(1)/(5)

The blue line passes through the points (-2,0) and (0,4). So, the slope of blue line is

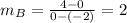
m_B=(4-0)/(0-(-2))=2

The slope intercept form of a line is

y=mx+b

Where m is slope and b is y-intercept.

The y-intercept of red line is 1 and slope is
-(1)/(5) .

y=-(1)/(5)x+1

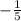Multiply both sides by 5.

5y=-x+5

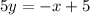
Add x on both the sides.

x+5y=5

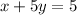
The related equation of red line is x+5y=5.

The shaded region is above the line and the related line is a solid line, therefore the sign of inequality is ≥. So, the first inequality is

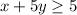
$x+5y\geq 5$

The y-intercept of blue line is 4 and slope is 2.

y=2x+4

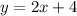
The related equation of blue line is y=2x+4.

The shaded region is below the line and related line is a solid line, therefore the sign of inequality is ≤. So, the second inequality is

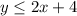
$y\leq 2x+4$

Therefore the correct option is 2.