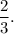Question

1. Consider this dilation.

(a) Is the image of the dilation a reduction or an enlargement of the original figure? Explain.
(b) What is the scale factor? Explain.

Answer 1

Answer: The answers are:

(a) The dilation is a reduction of the original figure.

(b) The scale factor of dilation is
`(2)/(3).`

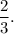
Explanation: We are given a dilation from ΔMSV to ΔM'S'V'.

We are to check whether the dilation is a reduction or an enlargement of the original figure. Also, to find the scale factor of dilation.

We know that if a figure is dilated to form the image figure, then the scale factor of dilation is given by

`S=\frac{\textup{length of a side of the dilated figure}}{\textup{length of the corresponding side of the original figure}}.`

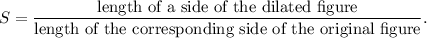
The dilation will be a reduction if S < 1 and it will be an enlargement if S > 1.

From the figure, we note that

the co-ordinates of the vertices of the original triangle MSV are M(-3, 3), S(6, 3) and V(3, -3),

and the co-ordinates of the dilated triangle M'S'V' are M'(-2, 2), S'(4, 2) and V'(2, -2).

So, the lengths of the corresponding sides MS and M'S' of both the original and dilated figures are calculated using distance formula as follows:

`MS=√((6+3)^2+(3-3)^2)=√(9^2)=9,\\\\M'S'=√((4+2)^2+(2-2)^2)=√(6^2)=6.`

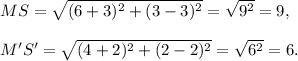
Therefore, the scale factor of dilation is given by

`S=(M'S')/(MS)\\\\\\\Rightarrow S=(6)/(9)\\\\\\\Rightarrow S=(2)/(3).`

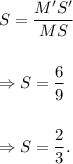
Since S < 1, so the dilation is a reduction.

Thus,

(a) The dilation is a reduction of the original figure.

(b) The scale factor of dilation is
`(2)/(3).`