Question

In △BCD, d = 3, b = 5, and m∠D = 25°. What are the possible approximate measures of angle B?

A. only 90°
B. only 155°
C. 20° and 110°
D. 45° and 135°

Answer 1

Option D. 45° and 135° is correct.

Explanation:

For better explanation of the solution, see the attached figure below :

Now, in ΔBCD

Take BC = d = 3 unit and CD = b = 5 unit,

And, ∠D = 25°,

So, By using sine law in the ΔBCD , We have

`(\sin 25)/(3)=(\sin B)/(5)\\\\\implies \sin B=5* (\sin 25)/(3) \\\\\implies \sin B=0.7043\\\\\implies B=44.78\approx 45`

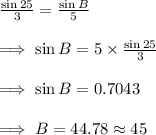
Hence, The approximate value of ∠B = 45°

Also, The exterior value of ∠B can be used by using linear pair property

⇒ ∠B = 180 - 45

⇒ ∠B = 135°

Therefore, Option D. 45° and 135° is correct.

Answer 2

Answer: D. 45° and 135°

Explanation:

Here, the BCD is a triangle,

In which BC = d = 3 unit and CD = b = 5 unit,

And, ∠D = 25°,

By the sin law,

`(sin B)/(5) = (sin 25^(\circ))/(3)`

`sin B = 5* (sin 25^(\circ))/(3)`

`sin B = (5 sin 25^(\circ))/(3)`

`sin B = 0.70436376956`

`B = 44.7781668526\approx 45^(\circ)`

Hence, the possible value of angle B is 45° ( approx) in the triangle,

While the value of the exterior angle B = 180° - 45° = 135° ( linear pairs )

⇒ Option D is correct.