Question

What is the difference between convergence and divergence? I'm in advanced algebra so try not to make a complicated answer. Thank you.

Answer 1

The concept of convergence is a topic more suited to a discussion of calculus if you want a fairly rigorous explanation.

But what it basically means is that, given a function that depends on one or more independent variables, the value of the function will "converge" or approach a finite value as the independent variable(s) approaches their own finite values.

Divergence means the opposite. If there is no finite or fixed value that a function appears to be approaching, then it does not converge, and is thus said to diverge.

Some examples: As
`x` gets arbitrarily large, the function


`f(x)=\frac1x`

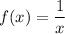
will approach 0. You can see why this must be the case by checking what happens to the value of
`\frac1x` when
`x` is picked to be 10, or 1000, or 1000000000, and so on. Clearly,
`\frac1x` must be positive, but the large the denominator, the smaller the value of
`\frac1x`. It will never actually take on the value of 0, but we can see that it must *converge to* 0.

On the other hand, the function


`f(x)=\sin x`

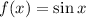
will oscillate indefinitely between the values of -1 and 1, so this function is said to not converge to any specific value as
`x` increases indefinitely, which means
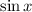
`\sin x` diverges.