Question

What is the probability that a point chosen at random in the given figure will be inside the larger circle and outside the smaller circle?

Enter your answer, as a fraction in simplest form, in the box.

P(inside larger circle and outside smaller circle) = _____

Answer 1

Answer:
`(40)/(49)`

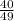
Explanation:

Given: The radius of the larger circle = 14 cm

The area of a circle is given by :-

`A=\pi r^2`

The area of the larger circle will be :-

`A=\pi (14)^2=196\pi cm^2`

The radius of the smaller circle = 6 cm

The area of the smaller circle will be :-

`A=\pi (6)^2=36\pi cm^2`

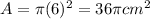
The area of the part which belongs to the the larger circle and outside the smaller circle =Area of larger circle- Area of smaller circle

`=196\pi-36\pi=160\pi cm^2`

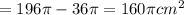
Now, the probability that a point chosen at random in the given figure will be inside the larger circle and outside the smaller circle is given by:-

`(160\pi)/(196\pi)=(40)/(49)`

Answer 2

The probability that a point is chosen at random in the given figure is 40/49 or .82. The answer to the following statement or the missing blank is 40/49. The probability is the possibility of the occurrence or happening of something.