Question

A truck is traveling at 74.5 kilometers per hour away from you. The driver is blowing the horn which has a frequency of 415 Hz. The speed of the sound is 346 m/s. What is the observed frequency of the sound?

Answer 1

fo = 335 Hzlet fo = frequency heard
f = actual frequency
v= speed of sound
vs = speed of source

For the first one,
fo = fv/(v - vs)
74.5 km/h = 20.69 m/s
vs = -20.69m/s since it is moving away from you

fo = (415Hz)(346m/s)/(346m/s - (-20.69m/s))
fo = 392 Hz

For the second one,
fo = fv/(v - vs)
82.8 km/h = 23 m/s
vs = 23m/s

fo = (312Hz)(331m/s)/(331m/s - (23m/s))

Answer 2

The observed frequency is 391.3 Hz.

Explanation:

Given : A truck is traveling at 74.5 kilometers per hour away from you. The driver is blowing the horn which has a frequency of 415 Hz. The speed of the sound is 346 m/s.

To find : What is the observed frequency of the sound?

Solution :

Let, f be the observed frequency

`f_0=415 hz` be the frequency heard

v=346 m/s be the speed of sound

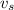`v_s` speed of truck

Distance traveled by truck
`d= 74.5 km = 74.5 * 1000`

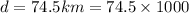
Time taken = 1 hour = 3600 sec.

We know,
`\text{Speed}=\frac{\text{Distance}}{\text{Time}}`

`v_s=(74.5 * 1000)/(3600)`

`v_s=20.69m/s`

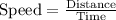
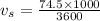
This is the Doppler effect.

The formula is given by,

`f=f_0((v)/(v+v_s))`

`f=415((346)/(346+20.69))`

`f=415((346)/(366.69))`

`f=415(0.943)`

`f=391.345`

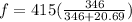
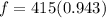
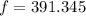
Therefore, The observed frequency is 391.3 Hz.