Answer: A.
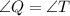
Explanation:
In the given figure we have two triangles ΔPQR and ΔSTQ.
Given :
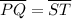
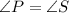
To prove both the triangles congruent we need
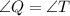 because by this we can use ASA congruence postulate to prove both the
because by this we can use ASA congruence postulate to prove both the
triangles congruent.
ASA postulate says that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.