Question

Rylan is calculating the standard deviation of a data set that has 9 values. He determines that the sum of the squared deviations is 316. What is the standard deviation of the data set? Round the answer to the nearest tenth

Answer 1

6.3

Explanation:

We have been given that Rylan is calculating the standard deviation of a data set that has 9 values. He determines that the sum of the squared deviations is 316.

We will use the formula
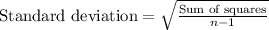`\text{Standard deviation}=\sqrt{\frac{\text{Sum of squares}}{n-1}}`, where n represents the number of data points in a data set.

Upon substituting our given values in above formula we will get,

`\text{Standard deviation}=\sqrt{(316)/(9-1)}`

`\text{Standard deviation}=\sqrt{(316)/(8)}`

`\text{Standard deviation}=√(39.5)`

`\text{Standard deviation}=6.284902544988\approx 6.3`

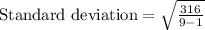
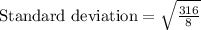
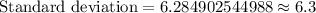
Therefore, the standard deviation of our given data set is 6.3.

Answer 2

The formula for the sum of the squares of the deviations is
SS = s² (N -1)

We are given
SS = 316
N = 9

Substituting
316 = s² (9 - 1)
Solving for s
s = 6.28

The standard deviation is 6.28