Question

A fair coin is tossed (heads or tails) 8 times. What is the probability that the coin will land "heads" exactly 4 out of the 8 times?

Answer 1

P = 0.273

Step-by-step explanation:

The probability to get exactly 4 heads can be calculated using the binomial distribution because we have n identical events with a probability p of success. So, we can use the following equation:

`P(x)=\text{nCx }\cdot p^x\cdot(1-p)^(n-x)`

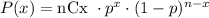
Where n is the number of times that the coin is tossed, x is the number of heads and p is the probability to land heads.

Additionally, nCx is calculated as:

`\text{nCx}=(n!)/(x!(n-x)!)`

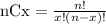
So, replacing n by 8, x by 4, and p by 0.5, we get:

`8C4=(8!)/(4!(8-4)!)=70`
`\begin{gathered} P(4)=70\cdot0.5^4\cdot(1-0.5)^(8-4) \\ P(4)=70\cdot0.5^4\cdot0.5^4 \\ P(4)=0.273 \end{gathered}`

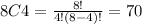
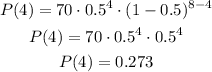
Therefore, the probability that the coin will land heads 4 times is 0.273