Question

find the measure of a complementary angle, a supplementary angle, and a vertical angle for the following measures:• m(

Answer 1

Supplementary angles are those that when summed, add up 180°. Two angles are complementary when they add up 90°.

Vertical angles are opposed by the vertex when two lines intersect each other. Vertical angles have always the same measure.

Now, following that logic, we can evaluate the two options.

1. m(∠A) = 45:

A supplementary angle will sum 180° when added to 45. Let's call that supplementary angle S1:

`\begin{gathered} 45^o+m(\angle S_1)=180^o \\ m(\angle S_1)=180^o-45^o \\ m(\angle S_1)=135^o \end{gathered}`

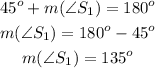
The measure of a supplementary angle will be 135°.

Similarly, let's call that complementary angle C1:

`\begin{gathered} 45^o+m(\angle C_1)=90^o \\ m(\angle C_1)=90^o-45^o \\ m(\angle C_1)=45^o \end{gathered}`

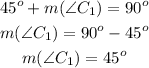
The measure of a complementary angle will be also 45°.

For the vertical angle, we stated that vertical angles are equal; then it will also be 45°.

For the second option we follow exactly the same process:

1. m(∠A) = 45:

A supplementary angle S2:

`\begin{gathered} w^o+m(\angle S_2)=180^o \\ m(\angle S_2)=180^o-w^o \end{gathered}`

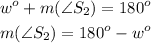
180° - w° will be a supplementary angle.

A complementary angle C2:

`\begin{gathered} w^o+m(\angle C_2)=90^o \\ m(\angle C_2)=90^o-w^o \end{gathered}`

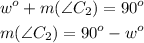
90° - w° will be a complementary angle.

And for the vertical angle, just like before, it will have exactly the same measure: w°.