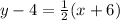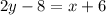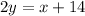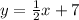By definition, if two lines share the same gradient, they are said to be parallel. So, we know for this equation, it must have a gradient of 1/2.
Now, since the point (-6, 4) passes through the line, we know it must satisfy the equation. Since we have a gradient/slope and a point, we can use the point-gradient form:
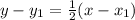
, where
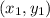
represents the points being passed through.