Question

An angle bisector of a triangle divides the opposite side of the triangle into segments 5 cm and 3 cm long. A second side of the triangle is 7.6 cm long. Find the longest and shortest possible lengths of the third side of the triangle. Round answers to the nearest tenth of a centimeter.

Answer 1

Let ABC be the triangle and AD be the angle bisector. Let BD=6 and DC=5 |dw:1359393342358:dw| Do you understand the figure?

Answer 2

Longest possible length of III side of triangle =12.7cm

shortest possible length of III side of triangle =4.6cm .

Explanation:

Given , an angle bisector of triangle divides the opposite side of triangle into segments 5cm and 3cm long.

In figure I

AB=a, BD=5cm , DC=3cm AC=b

If AB is second side Then AB=7.6cm

Third side=AC=b

Angle bisector theorem : when a ray bisect an angle of tiangle then it divides the opposite side of triangle into two segments which are proportinal to other two sides of the triangle.

Now, by angle bisector theorem

`(a)/(5) =(b)/(3)`

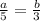
a=7.6 cm

`(7.6)/(5) =(b)/(3)`

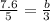
By cross multiply we get

`b=(7.6* 3)/(5)`

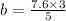
b=4.6cm

III side of triangle =4.6cm

In II figure

we take II side AB=a=7.6 cm

III side=b

Again , by using bisector angle theorem

`(b)/(5) =(7.6)/(3)`

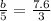
By cross multiply

`b=(7.6* 5)/(3)`

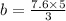
b=12.7 cm

Hence, the longest possible length of III side of triangle =12.7cm

the shortest possible length of III side of triangle =4.6 cm