Question

If you pick a gumball at random, put it back, and then pick another gumball at random, what is the probability of picking a blue gumball then picking a yellow gum ball? A) 1/25 B) 1/50 C)3/100 D) 3/10 There are two blues, one yellow, one white, one orange, two red, one pink, one purple, one green

Answer 1

The answer is B) 1/50

Probability of picking Blue-2/10 which is 1/5

Probability of picking Yellow-1/10

1/5x1/10=1/50

Answer 2

Answer: The correct option is (B)
`(1)/(50).`

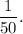
Step-by-step explanation: Given that there are two blue, one yellow, one white, one orange, two red, one pink, one purple and one green gumball.

We are to find the probability of picking a blue gumball then a yellow gum ball after replacing the first gumball.

The total number of gumballs is equal to the number of elements in the sample space for the event of picking a ball from the collection.

So,

`n(S)=2+1+1+1+2+1+1+1\\\\\Rightarrow n(S)=10.`

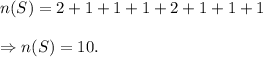
Let, E be the event of picking a blue gumball.

Then, n(E) = 2.

and let F be the event of picking a yellow gumball after putting the first ball back.

Then, n(F)=1.

Therefore, the probability of picking a blue gumball then a yellow gum ball after replacing the first gumball will be

`P\\\\=P(E)* P(F)\\\\\\=(n(E))/(n(S))* (n(F))/(n(S))\\\\\\=(2)/(10)*(1)/(10)\\\\\\=(1)/(50).`

Thus, the required probability is
`(1)/(50).`

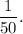
Option (B) is CORRECT.