Answer:


So then since we want the lesser root the correct answer on this case is:
D) 3
Explanation:
For this case we have the followin expression:
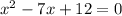
For this case we can use the quadratic formula in order to solve it, given by:
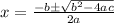
And on this case a = 1, b = -7, c = 12. And if we replace we got:


So then since we want the lesser root the correct answer on this case is:
D) 3