Question

A carpenter builds a rectangular bookcase that is 120 cm long and 62 cm tall. The carpenter uses two braces along the diagonals to support the bookcase. What is the length of the one of the braces, to the nearest tenth of a centimeter? Enter your answer as a decimal in the box. cm A rectangle. The width is labeled as 62 centimeters and the length is labeled as 120 centimeters. The diagonals are drawn that intersect each other.

Answer 1

check the picture below

is just a right-triangle, thus, use the pythagorean theorem, to get the hypotenuse, or diagonal's length

Answer 2

Length of the one of the braces is 135.07 centimeters.

Explanation:

Consider a rectangle ABCD with width is labeled as 62 centimeters and the length is labeled as 120 centimeters. The diagonals are drawn that intersect each other. (as shown in figure below )

We have to determine the length of diagonal.

Since, in a rectangle every angle is right angle that is 90°.

Using Pythagoras theorem in ΔABC,

`(AC)^2=(AB)^2+(BC)^2`

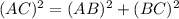
Putting values of AB = 120 and BC = 62, we get,

`(AC)^2=(120)^2+(62)^2`

`(AC)^2=+14400+3844`

`(AC)^2=18244`

`AC=√(18244)`

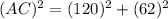
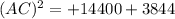
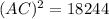
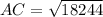
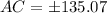`AC=\pm 135.07` (approx)

Since diagonal cannot be in negative, So ignoring negative value.

Length of the one of the braces is 135.07 centimeters.