Question

What is the area of the hemisphere with the removed object? Use Pi and round to the nearest tenth. I have answered this with 234.7 and this is not correct.

Answer 1

The area of the hemisphere is

`\begin{gathered} A=(1)/(2)(4*\pi* r^2)+\pi* r^2 \\ A=2*\pi* r^2+\pi* r^2 \\ A=3\text{ }\pi r^2 \end{gathered}`

Since r = 5 in, then

`\begin{gathered} A=3*\pi*(5)^2 \\ A=75\pi \end{gathered}`

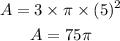
Now we need to subtract from it the 6 faces of the removable cube

The area of each face is

`a=s^2`

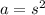
Where s is the edge of the cube

Since s = 3 in

Then the area of the 6 faces is

`\begin{gathered} T\mathrm{}a=6(3)^2 \\ T\mathrm{}a=6*9 \\ T\mathrm{}a=54 \end{gathered}`

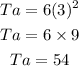
Now we will subtract it from the area of the hemisphere

`\begin{gathered} A=75\pi-54 \\ A=181.619449 \end{gathered}`

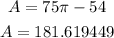
Round it to the nearest tenth

A = 181.6 square inches