
, because the parabola has the maximum, not the minimum, (∩)
The Vertex form of a parabola equation:
V(-3;4), so:
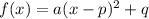
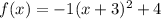
*
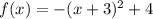
The zeros and the conix form of a parabola equation:

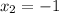
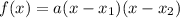
, so:
*
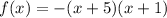
We can also use the general form of a parabola:
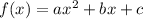
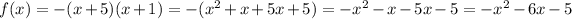
*
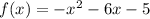 The answers: A, C, E
The answers: A, C, E
:)