Question

Matt Johnson takes out a mortgage for $240,000. There is a loan of 30 years at $1,200 per month. This gives a total interest of $192,000. What is the APR using the formula?

Answer 1

APR=((2×12×192,000)÷(240,000×361))×100
=5.32%

Answer 2

The APR is 4.38%.

Explanation:

Given : Matt Johnson takes out a mortgage for $240,000. There is a loan of 30 years at $1,200 per month. This gives a total interest of $192,000.

To find : What is the APR using the formula?

Solution : Formula of monthly payment

Monthly payment,
`M=\frac{\text{Amount}}{\text{Discount factor}}`

Discount factor
`D=(1-(1+i)^(-n))/(i)`

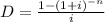
Where, Amount = $240,000

Monthly payment M=$1200

APR i =?

Time = 30 years

`n=30*12=360`

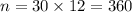
Monthly payment,
`M=\frac{\text{A}}{(1-(1+i)^(-n))/(i)}`

`M=(A* i)/(1-(1+i)^(-n))`

Substitute value,

`1200=(240000* i)/(1-(1+i)^(-360))`

`(1-(1+i)^(-360))/(i)=(240000)/(1200)`

`(1-(1+i)^(-360))/(i)=200`

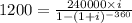
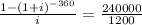
Solving using calculator,

`i=0.003655`

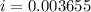
Now, In percentage and in months

`i=0.003655* 100* 12`

`i=4.38\%`

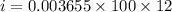
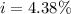
The APR is 4.38%.