Answer:
The population would reach
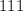 million in next
million in next
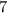 years
years
Explanation:
The initial population of Mexico was
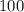 million
million
The growth rate of the population is
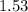 %per year
%per year
Then the future population of Mexico is given by
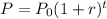
Where P = future population after t years
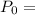 initial population
initial population
t = time period in years
Substituting the given vales in above equation we get
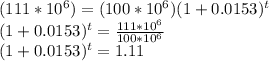
Taking log on both sides we get

≈
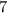 years
years
The population would reach
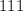 million in next
million in next
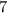 years
years