Question

Find the point(s on the surface z2=xy 1 which are closest to the point (7, 5, 0.

Answer 1

We're minimizing the function


`d(x,y,z)=√((x-7)^2+(y-5)^2+z^2)`

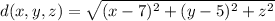
with respect to the constraint
`z^2=xy+1`. Recall that
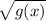
`√(g(x))`, where
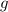
`g` is continuous, attains its extrema at the same points as
`g(x)`. This means we can work with
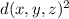
`d(x,y,z)^2` instead.

Using Lagrange multipliers: We have the Lagrangian


`L(x,y,z,\lambda)=(x-7)^2+(y-5)^2+z^2+\lambda(z^2-xy-1)`

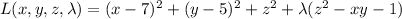
with partial derivatives


`\begin{cases}L_x=2(x-7)-\lambda y\\L_y=2(y-5)-\lambda x\\L_z=2z+2\lambda z\\L_\lambda=z^2-xy-1\end{cases}`

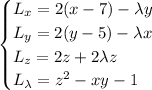
The third equation tells you that
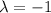
`\lambda=-1`, from which you can show that
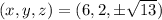
`(x,y,z)=(6,2,\pm√(13))` are the critical points.