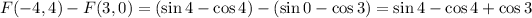Question

Evaluate the line integral, where c is the given curve. ?c sin(xdx cos(ydy c consists of the top half of the circle x2 y2 = 9 from (3, 0 to (-3, 0 and the line segment from (-3, 0 to (-4, 4.

Answer 1

You can parameterize the curve
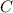
`C` and compute the integral along each component curve, or you can use the fact that
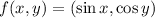
`f(x,y)=(\sin x,\cos y)` is the continuous gradient of a function
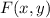
`F(x,y)` and observe that the line integral is path independent.

In other words, there is a function
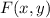
`F(x,y)` such that
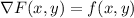
`\\abla F(x,y)=f(x,y)`, so the integral along any curve
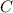
`C` from the points
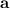
`\mathbf a` to
`\mathbf b` is simply


`\displaystyle\int_Cf(x,y)\,\mathrm dS=\int_C(P(x,y)\,\mathrm dx+Q(x,y)\,\mathrm dy)=F(\mathbf b)-F(\mathbf a)`

You have
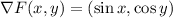
`\\abla F(x,y)=(\sin x,\cos y)`, and so


`(\partial F(x,y))/(\partial x)=\sin x\implies F(x,y)=-\cos x+g(y)`

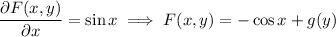
while


`(\partial F(x,y))/(\partial y)=\cos y=g'(y)\implies g(y)=\sin y+K`

where
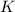
`K` is an arbitrary constant. So we've found that


`F(x,y)=\sin y-\cos x+K`

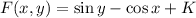
which means the line integral has a value of


`F(-4,4)-F(3,0)=(\sin4-\cos 4)-(\sin0-\cos3)=\sin4-\cos4+\cos3`