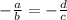Question

Can somebody please help me figure this out? I think the answer is d

In this diagram, which equation could you prove to be true in order to conclude that the lines are parallel?

−ab=−cd

−ab⋅−dc=−1

−ab⋅−cd=−1

−ab=−dc

Answer 1

Answer is -a/b = -d/c

Explanation:

Took the quiz!

Answer 2

For two lines to be parallel, their slope must be the same.
To find the slope, we can use the form:
`(y_1 - y_2)/(x_1 - x_2)`

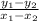
For the top line, the change in height (y value) can be seen as a - 0 or simply a, and the change in base is just -b (because our
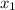
`x_1` is just 0, from the origin.

Hence, line 1's gradient is:
`-(a)/(b)`

Now, we can repeat this process for line 2:
Change in height is -d, change in base is c

Hence, line 2's gradient is:
`-(d)/(c)`

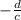
For the two lines to be parallel, both gradients must be the same:

`-(a)/(b) = -(d)/(c)`