Question

A transformation translates the point s(-11) down 2 units and right 3 units. What rule describes this translation?

Answer 1

f(s) = s(-11-3) - 2

the -3 is your shift 3 units to the right, and the -2 is your shift down.

Answer 2

`f(x,y)\rightarrow f(x+3,y-2)`

`s(-1,1)\rightarrow f(2,-1)`

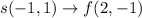
Explanation:

Given : A transformation translates the point s(-1,1) down 2 units and right 3 units.

To find : What rule describes this translation?

Solution :

When there is as shift of b unit downward means there is a shift in y by b unit.

f(x,y)→f(x,y-b) , shifting downward by b unit.

So, f(x,y)→f(x,y-2), shifting downward by 2 unit.

When there is as shift of a unit right means there is a shift in x by a unit.

f(x,y)→f(x+a,y) , shifting right by a unit.

So, f(x,y)→f(x+a,y), shifting right by 3 unit.

The rule of translation described is

`f(x,y)\rightarrow f(x+3,y-2)`

In the given point
`s(-1,1)\rightarrow f(-1+3,1-2)=f(2,-1)`