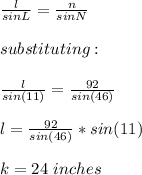Question

In ΔLMN, n = 92 inches, ∠N=46° and ∠L=11°. Find the length of l, to the nearest inch.

Answer 1

24 inches

Explanation:

A triangle is a polygon with three sides and three angles. The types of triangles are scalene triangle, equilateral triangle, right angled triangle and obtuse triangle.

Sine rule states that given a triangle with sides a, b, c and their corresponding angles opposite to the sides as A, B, C. Then:

`(a)/(sinA) =(b)/(sinB) =(c)/(sinC)`

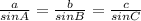
In triangle LMN:

We can find the length of l using sine rule:

`(l)/(sinL)=(n)/(sinN) \\\\substituting:\\\\(l)/(sin(11))=(92)/(sin(46)) \\\\l=(92)/(sin(46))*sin(11)\\\\k=24\ inches \\`