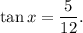Question

Given cos x =12/13 And sin x = 5/13
what is ratio for tan x

Answer 1

Its 5/12 you just divide sin by cos to get tan so divide 5/13 by 12/13 and you'll get tan

Answer 2

Answer: The ratio for
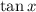`\tan x` is
`(5)/(12).`

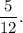
Step-by-step explanation: Given that

`\cos x=(12)/(13),\\\\\\\sin x=(5)/(13).`

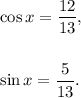
The tangent of an angle is given by the sine of that angle divided by the cosine of that angle.

So, for any angle 'x', we have

`\tan x=(\sin x)/(\cos x).`

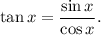
For the given values, the ratio of
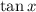`\tan x` can be calculated as follows:

`\tan x=(\sin x)/(\cos x)=((5)/(13))/((12)/(13))=(5)/(13)* (13)/(12)=(5)/(12).`

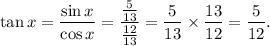
Thus, the ratio is given by

`\tan x=(5)/(12).`